Микроконтроллер и логические операции

Доброго дня уважаемые радиолюбители!
Приветствую вас на сайте “Радиолюбитель“

Логические операции и их применение

В нашей жизни бывают случаи когда нет необходимости вникать в глубину того, или иного вопроса, достаточно и его поверхностного понимания. Иногда это связано с нашим «нежеланием», в другом случае сложностью этого вопроса. Так и сейчас, изучая логические операции, мы не будем лезть в глубину, а просто смиримся с тем фактом, что они существуют и знать их надо.

Основа всего – слово «логика».
Логика (др.-греч. λογική) — «наука о правильном мышлении», «искусство рассуждения» (от λόγος — «речь», «рассуждение», «мысль»).
Как видите, логика это не просто древнегреческое слово, а целая наука, изучение которой позволяет нам правильно и здраво рассуждать, и, соответственно, делать правильные выводы из наших рассуждений, чего, однако, очень не хватает в нашем современном мире.
Рассуждая о чем-либо, мы, на основе логических заключений, делаем соответствующие выводы. К примеру, думая о своем товарище, на основе каких-то фактах, характеризующих его, мы можем сделать вывод – друг он нам, или нет (или: «и не друг, и не враг, – а так»).

В конце 19 века, группа лиц, под названием «математики», решила перевести весь наш мыслительный процесс в более понятную для них форму – математическую. И из простой, человеческой логики, появилась математическая или – символическая логика. То есть, по их разумению, найти истину можно не только путем шевеления «серым веществом», но и применением математических методов. В чем суть этого метода. Любая высказанная нами мысль основывается на каких то фактах – кирпичиках, составляющих ее основу. Так вот, в математической логике эти «кирпичики» имеют только два состояния – «ложь» или «истина». По идее, и в человеческой логике должно быть также. Но на то мы и «человеки».
1+1 равно 2 – истинна, 1+1 не равно 2 – ложь. Все просто и понятно. Но это только в математической логике, а у людей 1+1 может равняться и 3. Так вот, из этих «кирпичиков», а у математиков они называются – «простые выражения», которые могут быть только или «истинной», или «ложью», складываются «сложные выражения», которые, естественно, тоже могут быть только или «истинными» или «ложными». А весь этот процесс получения сложного выражения из простых можно описать «логической формулой» или, как еще говорят, – «логическим выражением».
И вот тут мы подошли к главному – к логическим операциям:
Логическое выражение – это символическая запись высказывания, состоящая из логических величин, объединенных логическими операциями. Логические величины – это или «1», или «0». Если выражение «истинно» – то его величина 1, если «ложно» – то его величина 0 (так уж принято).
Логические операции позволяют складывать, а точнее – связывать, между собой простые выражения (те самые «кирпичики») – логические величины.
К примеру, перефразируя Уильяма, нашего, Шекспира, возьмем вот такое предложение:
«Изучим или не изучим (микроконтроллер), вот в чем вопрос».
Слово «изучим» обозначим как «А», «не изучим» – как «В» и посмотрим как это предложение может выглядеть в символьной записи с использование логической операции:
А or В = ?

Точно также происходит запись логических операций при создании программы. Каждый “язык” программирования имеет соответствующий набор символьных команд, с помощью которых происходит запись логических операций в программе.

Ну а теперь я постараюсь ответить на вопрос – «Зачем нам, простым смертным, далеким от этих философских и математических понятий, это нужно».
Во-первых. Лишними любые знания никогда не бывают. Познавая новое, мы открываем для себя что-то неизвестное, расширяем свой кругозор, пополняем свой скудный словарный запас (что позволяет более внятно излагать свою мысль, а не прибегать через слово к нецензурным связкам для ее озвучивания), а самое главное – учимся мыслить другими, более высокими категориями, тем самым отдаляя себя от «прародителей» – обезьян.
Во-вторых. Труд математиков не пропал даром и не остался только теорией.
Все современные цифровые технологии основываются на логических операциях, без них никуда не деться. Почти все (а может даже и все) цифровые микросхемы в своей работе используют логические схемы (выполняют логические операции, в том числе и микроконтроллер).
Теперь конкретно для нас, изучающих микроконтроллеры и их программирование:
1. Создавая программу, мы прописываем все действия микроконтроллера основываясь на своей логике с применением логических операций, иногда даже и не подозревая об этом (теперь-то, мы не только «не подозреваем»), которые применяем к логическим выражениям.
Пример – «если в ходе выполнения программы получен такой результат, то дальше программа пойдет вот таким путем, а если мы получили другой результат, то программа дальше пойдет вот этим путем» – типичное выполнение логической операции.
2. В программировании логическая операция применяется не только к логическому выражению (смотри п.1), но и для операций с двоичными числами, так называемые «логические побитовые (битовые) операции», которые очень сильно облегчают тяжелую жизнь программиста (этот пункт мы детально рассмотрим при изучении команд микроконтроллера).
3. Нельзя создать конструкцию только на одном микроконтроллере. Она будет бессмысленна. Помимо самого микроконтроллера в схеме должна быть его «обвязка», – резисторы, конденсаторы, диоды, транзисторы, индикаторы, реле и т.д. Очень часто в схемах на микроконтроллерах применяются цифровые микросхемы, в основе работы которых лежит принцип логических операций. Знание логических операций и грамотное применение таких микросхем совместно с микроконтроллером, позволяет создавать более простые и эффективные радиолюбительские конструкции.

Существует три основных логических операции при помощи которых можно записать любое логическое выражение (вот тут, надо сосредоточиться):

1. Инверсия
2. Конъюнкция
3. Дизъюнкция

Конъюнкция, оно же «Логическое И», оно же «Логическое умножение».
Мы выбираем название «Логическое И» – оно чаще встречается в программировании.
Допустим, у нас есть два простых выражения – А и В. Эти выражения могут иметь значения или 1 (истина), или 0 (ложь). При выполнении операции «Логическое И» мы получим сложное выражение которое примет значение 1 (истина) только в том случае если и А, и В имеют значение 1 (истина), во всех других случаях результат будет 0 (ложь).
Операция «Логическое И» имеет обозначения (в языках программирования): И, &&, AND, &.
Посмотрите на таблицу (такие таблицы называются «таблицы истинности»):
А    В   А&В
1     1      1
0    0      0
1     0     0
0     1     0
Как видите, результат будет «истинной», равным 1, если только и А, и В будут равны 1 (истинны).
К примеру, прописывая алгоритм работы программы, мы можем эту операцию «озвучить» так: «Если в ходе выполнения программы результаты А и В «истинны», то дальше выполняем это, если результаты А и В, оба, или один из них – «ложь», то дальше выполняем вот это».
А третье название операции – «Логическое умножение» (не путайте с арифметическим умножением) применяется для двоичных чисел.

Дизъюнкция, оно же «Логическое ИЛИ», оно же «Логическое сложение».
Мы выбираем название «Логическое ИЛИ». Кстати, если логически подумать, то можно и догадаться какие результаты будут при выполнении этой операции.
В «Логическом И» результат равен 1, если и А, и В, равны 1, а в «Логическом ИЛИ» результат будет равен 1, если или А, или В, равны единице.
Операция «Логическое ИЛИ» имеет обозначения: ИЛИ, ||, OR, |.
Посмотрим таблицу истинности:
А    В    А||В
1     1       1
0    0       0
1     0       1
0     1       1
А «Логическое сложение» применяется ….. Я думаю вы догадались где.

Инверсия, оно же «Логическое НЕ», оно же «Отрицание».
Мы выбираем название «Логическое НЕ».
Операция «Логическое НЕ» имеет обозначения: НЕ, !, NOT.
Тут вообще все просто:
Если А=1 (истина), то после выполнения операции «Отрицание» А примет значение 0, то есть становится ложным. И наоборот.
Есть еще одно название этой операции «Инвертор», а применяется оно в отношении цифровых микросхем.

В программировании часто применяется еще одна логическая операция – симбиоз «Логического И» и «Логического ИЛИ»:
Строгая дизъюнкция, оно же «Исключающее ИЛИ», оно же «Логическое сложение, исключающее ИЛИ», оно же «Сложение по модулю 2»
Мы выбираем название «Исключающее ИЛИ»
Операция «Исключающее ИЛИ» имеет обозначения: Искл.ИЛИ, XOR, ^.
Таблица истинности
А    В    АxorВ
1     1        0
0    0        0
1     0        1
0     1        1
В этом случае, при выполнении операции «Исключающее ИЛИ», результат будет истинен (равен 1), если А не равно В.  В остальных случаях результат будет равен 0 (ложный).

Как я уже говорил, логические операции применяются не только к выражениям, но и к двоичным числам – так называемые логические побитовые (битовые) операции. А повторяюсь я только потому, что в некоторых языках программирования логические операции с выражениями, и логические битовые операции имеют одинаковое написание, и если вы будете пользоваться таким языком, то этот момент надо всегда держать в памяти, чтобы не допустить ошибок.

Также мы уяснили, что логические операции – основа цифровой техники. Даже цифровые микросхемы, которые предназначены только для выполнения логических операций, называют – «логические микросхемы», или еще проще – «логика».
Немного остановимся на микросхемах логики и мы.
Работы цифровых микросхем логики основана на выполнение трех основных логических операций, с которыми мы ознакомились выше. Сочетание этих логических операций позволило создать великое (ну, может и не совсем великое) множество цифровых микросхем логики.
Основа таких микросхем – логический элемент:
Логические элементы — устройства, предназначенные для обработки информации в цифровой форме.
Логические элементы выполняют логическую функцию (операцию) над входными сигналами (операндами, данными).

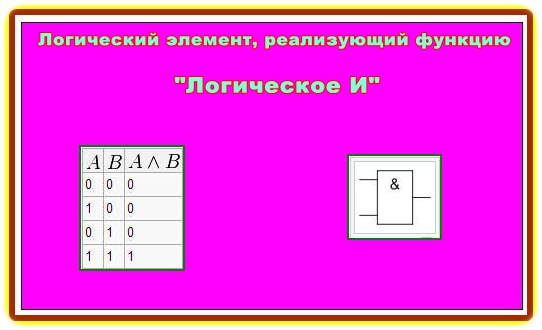
1. Логический элемент выполняющий операцию «Логическое И»:
Логический элемент, реализующий функцию конъюнкции («Логическое И»), называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:
– «1» тогда и только тогда, когда на всех входах действуют «1»,
– «0» тогда и только тогда, когда хотя бы на одном входе действует «0»

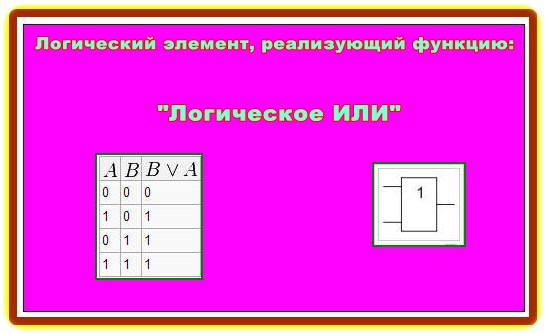
2. Логический элемент, реализующий функцию «Логическое ИЛИ»:
Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:
– «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,
– «0» тогда и только тогда, когда на всех входах действуют «0»

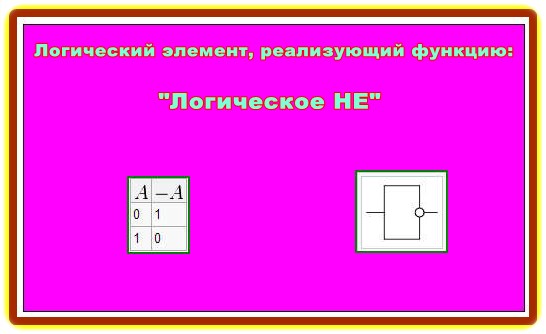
3. Логический элемент, реализующий функцию «Логическое НЕ»:
Мнемоническое правило для отрицания звучит так: На выходе будет:
– «1» тогда и только тогда, когда на входе «0»,
– «0» тогда и только тогда, когда на входе «1»

Это основные логические элементы.
А вот примеры комбинации основных логических операций:

1. Логический элемент, реализующий функцию «Исключающее ИЛИ» (неравнозначность):
Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:
– «1» тогда и только тогда, когда на входе действует нечётное количество,
– «0» тогда и только тогда, когда на входе действует чётное количество
Словесное описание: “истина на выходе – только при истине на входе 1, либо только при истине на входе 2″.

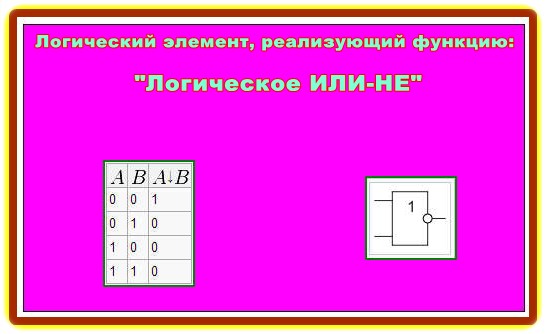
2. Логический элемент, реализующий функцию «Логическое ИЛИ-НЕ» (инверсия функции дизъюнкции):
Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:
– «1» тогда и только тогда, когда на всех входах действуют «0»,
– «0» тогда и только тогда, когда хотя бы на одном входе действует «1»

3. Логический элемент, реализующий функцию «Логическое И-НЕ»:
Мнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:
– «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,
– «0» тогда и только тогда, когда на всех входах действуют «1»

Кроме таких комбинаций логических операций существует еще много других.

Практический пример использования микросхем логики.
Допустим, собираем охранную сигнализацию для дома. У нас имеется четыре датчика (на дверь и три окна). При срабатывании любого из них должен срабатывать звуковой сигнал.
Без применения дополнительных микросхем нам придется подключить эти четыре датчика к четырем входам микроконтроллера. Затем, программным путем, проверять каждый из четырех входов на наличие сигнала срабатывания датчика. При использовании микросхемы логики, выполняющую «Логическую операцию ИЛИ» и имеющую четыре входа, к примеру К561ЛЕ6 (в данной микросхеме имеется 3 логических четырехвходовых элементов, реализующих логическую функцию «ИЛИ-НЕ»), мы можем подключить датчики к входам одного элемента микросхемы, а единственный его выход подключить к одному входу микроконтроллера. Теперь, при срабатывании любого датчика на выходе микросхемы сформируется сигнал срабатывания, который подастся на вход микроконтроллера. Наш выигрыш:
– задействован всего один вход микроконтроллера (вместо четырех)
– уменьшается объем программы (вместо опроса четырех входов, нам надо контролировать только один вход микроконтроллера).

Кстати, есть еще одна разновидность логики – женская логика. Весьма интересная штука. Но так как она к сегодняшней теме не относится, то придется, к сожалению, этот вопрос опустить.

---

Предыдущие статьи:

♦ Микроконтроллер и как его победить
♦ Микроконтроллер и системы счисления

Следующие статьи:

♦ Общее устройство микроконтроллера
♦ Арифметико-логическое устройство и организация памяти – память программ, память данных, энергонезависимая память
♦ Регистры общего назначения, регистры ввода/вывода, стек, счетчик команд
♦ Регистр состояния SREG
♦ Порты ввода/вывода микроконтроллера

---

---