Микроконтроллер и системы счисления
Доброго дня уважаемые радиолюбители!
Приветствую вас на сайте “Радиолюбитель“
Системы счисления применяемые при создании программ для микроконтроллеров
Хочется нам, или нет, уважаемые читатели, но постигая азы программирования микроконтроллеров, нам придется немного расшевелить свое «серое вещество», вернуть на место «шарики», которые иногда заходят за «ролики», смазать их (можно Сникерсом) и затолкать в свою безразмерную память (но не слишком глубоко) некоторые новые знания, без которых не обойтись.
Итак, системы счисления, что это такое и зачем нам это нужно знать.  Как всегда, умное определение:
Как всегда, умное определение:
Система счисления – символический метод записи чисел, представление чисел с помощью письменных знаков (думаем «Один», а записываем «1»).
Хотя бывает, особенно у людей с загребущими лапами, что думают «Один”, а записывают «О». В среднем, обычный россиянин знаком с двумя такими системами, а пользуется в своей ежедневной практике только одной (больше и не надо). Мы все знаем римскую систему счисления под названием – “римские цифры” (еще со школьной поры) и, родную и близкую нам, – десятичную систему счисления.
Десятичная система счисления – набор цифр от 0 до 9, из комбинации которых составляются любые числа. Римская система счисления – всем нам знакомый набор палочек и латинских букв – I, IV, L, D и так далее.
Например, вот так выглядит символическая запись нынешнего года:
– в десятичной системе – 2014
– в римской системе – ММХIV
Вспомнили? И хорошо.
А знаете ли вы, что до начала ХIX (19) века, на Руси существовала пятеричная система счисления, так называемый «счет на пятки” (с ударением на “и”)? К примеру, число «десять», звучало как «два-пять”.
Почему мы вдруг заговорили о «циферках»? Дело в том, что как вы наверное уже и сами догадались из предыдущих статей, микроконтроллер не понимает привычные нам наборы цифр (вспоминайте – все команды для него состоят из набора только двух цифр: нуля и единицы), а общаться с ним надо.
Для общения с микроконтроллером (да и вообще со всей микропроцессорной, цифровой техникой) существует двоичная система счисления. В двоичной системе счисления все числа записываются только двумя символами – «0» и «1». Почему для цифровой техники выбрана именно двоичная система счисления. А дело в том, что своих «мозгов» у цифровой технике нет, и распознают они цифры не глазами, а уровнями напряжения на своих входах. Для распознавания «0» и «1» достаточно двух уровней напряжения (а если бы пользовались десятичной системой счисления, то понадобилось бы уже десять уровней напряжения).
Принято считать, что:
- цифре «1» соответствует высокий уровень напряжения
– цифре «0» соответствует низкий уровень напряжения.
К примеру, если на «ножку» микроконтроллера (при напряжении его питания равном 5 вольтам) подать 5 вольт, то он поймет, что это «1», а если ничего не подать, а замкнуть «ножку» на «землю», то он поймет, что это «0». Также и в обратном порядке. Если микроконтроллер должен передать «1» то он выставляет на своей «ножке» высокое напряжение – 5 вольт, а если «0» – то низкое напряжение – 0 вольт. То есть, распознание цифр 0 и 1 в цифровой технике происходит двумя уровнями сигнала.
Интересно, что вывод микроконтроллера может иметь еще и третье состояние – и не «0», и не «1», а так называемое «Z- состояние». То есть, на «ножке» и не «высокое», и не «низкое” напряжение. В этом случае вывод микроконтроллера считается отключенным. Физически, в «Z- состояние», вывод конечно ни от чего не отключается, просто на нем в этот момент выставляется напряжение, которое не соответствует ни низкому, ни высокому напряжению. Дело в том, что высокое напряжение, при котором микроконтроллер однозначно определяет, что это «1», не соответствует строго 5 вольтам, а может находиться в некотором промежутке: от 2,5 до 5 вольт. А низкое напряжение, при котором микроконтроллер однозначно определяет, что это «0», не должно быть выше 0,5 вольт. Если напряжение на «ножке” микроконтроллера будет больше 0,5 вольт, но меньше чем 2,5 вольт, то микроконтроллер не сможет распознать «0» это, или «1». Это и есть третье состояние «Z – состояние» – напряжение на «ножке» вроде есть, но микроконтроллер на него никак не реагирует.
В цифровой технике высокий уровень напряжения, соответствующий «1», называют – логическая единица, а низкий уровень напряжения, соответствующий «0», называют логическим нулем.
Давайте посмотрим, как числа десятичной системы соответствуют числам в двоичной системе:
1 – 1
2 – 10
3 – 11
5 – 101
10 – 1010
200 – 11001000
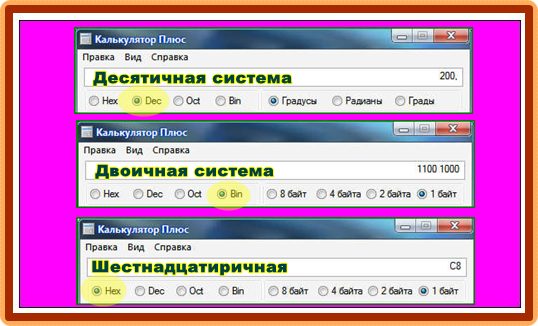
Перевести число из десятичной системы в двоичную и обратно, очень просто. Достаточно иметь калькулятор с инженерными функциями, или воспользоваться стандартным калькулятором «Windows», переведя его в «инженерный режим»:
Чтобы не путать числа десятичной системы с числами двоичной системы, в последних, в конце числа дописывают символ: «В»
200 – 11001000В
В языках программирования такие символы добавляют в начало числа.
200 – 0b11001000, или
200 – #b11001000
Десятичные числа в языках программирования записываются как обычно, без всяких добавлений. Но а в не «языка программирования», к ним может дописываться буква «D»:
200D – 0b11001000
И еще, если пользуясь числами в десятичной системе, мы говорим, например «пять», то в двоичной системе мы должны говорить не «сто один», а «один-ноль-один».
Арифметические операции в двоичной системе счисления. В двоичной системе с числами можно вытворять тоже самое, что и в десятичной:
– складывать
– вычитать
– умножать
– делить
Естественно, что для выполнения арифметических операций над двоичными числами мы с успехом можем воспользоваться и калькулятором, но знать, как это делается ручкой на бумаге – полезно, пригодится. Мы рассмотрим для примера только две операции – сложение и умножение. Они проще для понимания, а в дальнейшем, если потребуется то рассмотрим и остальные операции (но вы можете это сделать и самостоятельно).
Сложение.
Сложение производится в столбик также как и с десятичными числами.
Правила, которые надо соблюдать при сложении:
0+0 = 0
0+1 = 1
1+0 = 1
1+1 = 10 – в этом случае процесс сложения происходит также как, к примеру, и при сложении 5+5 в десятичной системе – «пять плюс пять равно десять, ноль пишем, один «на ум» пошло» То, что пошло «на ум», потом мы переносим в следующий разряд.
Для двоичной системы: «один плюс один равно один-ноль, ноль пишем, один «на ум» пошло».
Для примера:
– в десятичной: 5+5 = 10
– в двоичной: 101+101 = 1010, а теперь в столбик:
101
+
101
Начинаем справа-налево (как обычно):
1+1 = 10, 0 пишем, 1 на «ум пошло» (….0)
0+0 = 0 + 1 с «ума берем» = 1 (….10)
1+1 = 10 так и пишем 10 (1010)
и получаем итог: 1010, что равно 10 в десятичной системе.
Умножение.
Правила, которые надо соблюдать при умножении:
0х0 = 0
0х1 = 0
1х0 = 0
1х1 = 1
На примере:
– в десятичной системе:
5х5 = 25
– в двоичной системе:
101х101 = 11001
А теперь в столбик (все по обычным законам математики):
101
х
101 ——-
101 - умножаем 1 на 101
000 - умножаем 0 на 101
101 - умножаем 1 на 101
——–
11001
– все строчки складываем, и получаем результат 25.
Интересно, что при программировании в микроконтроллере операции умножения (не все микроконтроллеры могут самостоятельно умножать, но все умеют складывать и отнимать), результат находят не так, как мы это проделали выше, а по другому – намного проще. А как это делается мы узнаем в процессе изучения команд микроконтроллера.
Кроме десятичной и двоичной системы счисления, в цифровой технике применяется еще одна, третья, система счисления - шестнадцатиричная. В шестнадцатиричной системе счисления все числа обозначаются не десятью символами, как в десятичной, и не двумя, как в двоичной, а шестнадцатью: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Посмотрим соответствие чисел шестнадцатиричной системы по отношению к десятичной и двоичной:
1 – 1 – 1
5 – 101 – 5
10 – 1010 – А
200 – 11001000 – С8
Для обозначения шестнадцатиричных чисел в конце дописывают латинскую букву «Н»:
1Н, 5Н, АН, С8Н
Для записи шестнадцатиричных чисел в языках программирования, им в начале добавляют «Ох» или знак «$» (и здесь «зеленый» отметился):
С8 = С8Н = ОхС8 = $С8
Почему в языках программирования применяют аж целых три вида систем счисления:
– десятичную
– двоичную
– шестнадцатиричную
ведь все равно, в ходе перевода программы в машинные коды, они все принимают вид только двоичной системы? В принципе, можно обойтись только десятичными цифрами – для нас так будет удобнее, или двоичными – чтобы не мучить компилятор переводом чисел в двоичную систему из других систем. Но все дело в том, что и в системе команд, и инструкциях, которые должен выполнять микроконтроллер, в разных случаях приходится пользоваться числами и в двоичной системе, и в шестнадцатиричной. В одних случаях для наглядности, а в других случаях – чтобы не усложнять себе жизнь (если что-то известно в виде числа в шестнадцатиричной системе, то зачем делать лишние телодвижения и переводить это число в десятичную систему, если только для наглядности). Но смею вас заверить, что только на первых порах вы будете ощущать некоторый дискомфорт при использовании двоичной и шестнадцатиричной систем счисления, через короткое время вы уже не будете обращать на это внимание. А может другая система счисления вам понравится настолько, что и в повседневной жизни перейдете на нее. Круто будет, сказать в магазине продавцу – «Вы мне недодали 3FF рублей». Кстати, фанаты «нетрадиционной» системы счисления, даже создают электронные часы, которые показывают время в двоичной системе (Сколько время? 1-1-0-0-1-0-1-1).
В следующей статье мы с вами разберем еще один, более «темный лес» – логические операции. Но а после этого уже перейдем к изучению устройства микроконтроллеров.
Предыдущие статьи:
♦Микроконтроллер и как его победить
Следующие статьи:
♦ Микроконтроллер и логические операции
♦ Общее устройство микроконтроллера
♦ Арифметико-логическое устройство и организация памяти – память программ, память данных, энергонезависимая память
♦ Регистры общего назначения, регистры ввода/вывода, стек, счетчик команд
♦ Регистр состояния SREG
♦ Порты ввода/вывода микроконтроллера