Расчет фильтров верхних и нижних частот
Практический расчет фильтров верхних и нижних частот (RC и LC фильтров)
Доброго дня уважаемые радиолюбители!
Сегодня, на сайте “Радиолюбитель”, на очередном занятии “Практикума начинающего радиолюбителя”, мы с вами рассмотрим порядок расчета фильтров верхних и нижних частот.
 Из этой статьи вы узнаете, что фильтровать можно не только “базар”, но и многое другое. А изучив статью, научитесь самостоятельно проводить необходимые расчеты, которые вам помогут при конструировании или наладке различной аппаратуры (в статье много формул, но это не страшно, на самом деле все очень просто).
Из этой статьи вы узнаете, что фильтровать можно не только “базар”, но и многое другое. А изучив статью, научитесь самостоятельно проводить необходимые расчеты, которые вам помогут при конструировании или наладке различной аппаратуры (в статье много формул, но это не страшно, на самом деле все очень просто).
Фильтры верхних частот (далее ФВЧ) и фильтры нижних частот (далее ФНЧ) применяются во многих электрических схемах и служат для разных целей. Одним из ярких примеров их применения – цветомузыкальные устройства. К примеру, если вы наберете в поисковике “простая цветомузыка”, то заметите, насколько часто в результатах поиска показывается простейшая цветомузыка на одном транзисторе. Естественно, что такую конструкцию очень трудно назвать цветомузыкой. Зная что такое фильтры верхних и нижних частот и как они рассчитываются, вы сами, самостоятельно, можете переделать такую схему в более полноценное цветомузыкальное устройство. Простейший случай: вы берете две таких одинаковых схемы, но перед каждой ставите фильтр. Перед одним транзистором ФНЧ, а перед вторым – ФВЧ и у вас уже получается двухканальная цветомузыка. А если покумекать, то можно взять еще один транзистор и применив два фильтра (ФНЧ и ФВЧ или один средней частоты) получить третий канал – среднечастотный.
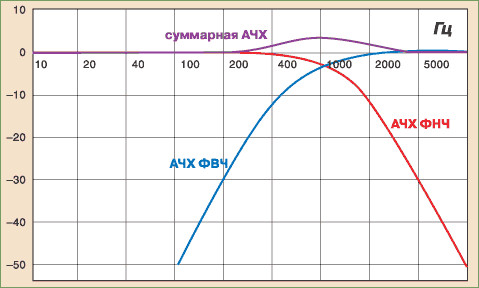
Прежде чем продолжить разговор о фильтрах коснемся очень важной их характеристики – амплитудно-частотная характеристика (АЧХ). Что это за показатель.
Т.е., на одной частоте входящего на фильтр сигнала уровень амплитуды такой-же как и на выходе, а для другой частоты, фильтр, оказывая сопротивление сигналу, ослабляет амплитуду входящего сигнала.
Тут же появляется еще одно определение: частота среза.
Например, если при частоте входного сигнала 1 кГц амплитудой 1 вольт на выходе фильтра амплитуда входного сигнала уменьшается до 0,7 вольта, то частота 1 кГц является частотой среза данного фильтра.
И последнее определение – крутизна частотной характеристики фильтра.
Фильтры высоких и низких частот – это обыкновенные электрические цепи, состоящие из одного или нескольких элементов, обладающих нелинейной АЧХ, т.е. имеющих разное сопротивление на разных частотах.
Подытоживая вышесказанное можно сделать вывод, что по отношению к звуковому сигналу фильтры являются обыкновенными сопротивлениями, с тем лишь отличием, что их сопротивление меняется в зависимости от частоты звукового сигнала. Такое сопротивление называется реактивным и обозначается как Х.
Частотные фильтры изготавливают из элементов, обладающих реактивным сопротивлением – конденсаторов и катушек индуктивности. Рассчитать реактивное сопротивление конденсатора можно по нижеприведенной формуле:
Xc=1/2пFС где:
Хс – реактивное сопротивление конденсатора;
п – оно и в Африке “пи”;
F – частота;
С – емкость конденсатора.
То есть, зная емкость конденсатора и частоту сигнала, всегда можно определить какое сопротивление оказывает конденсатор для конкретной частоты.
А реактивное сопротивление катушки индуктивности вот этой формулой:
XL=2пFL где:
XL – реактивное сопротивление катушки индуктивности;
п – оно и в России “пи”;
F – частота сигнала;
L – индуктивность катушки
Частотные фильтры бывают нескольких типов:
– одноэлементные;
– Г- образные;
– Т – образные;
– П – образные;
– многозвенные.
В этой статье мы с вами не будем глубоко опускаться в теорию, а рассмотрим только поверхностные вопросы, и только фильтры состоящие из сопротивлений и конденсаторов (фильтры с катушками индуктивности трогать не будем).
Одноэлементный фильтр
- фильтр состоящий из одного элемента: или конденсатора (для выделения верхних частот), или катушки индуктивности (для выделения нижних частот).
Г – образный фильтр
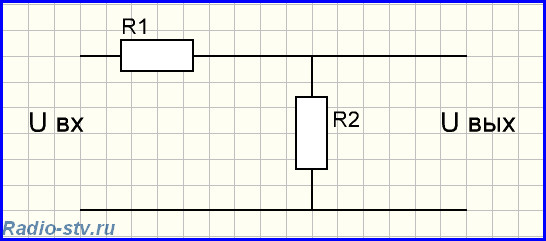
Г-образный фильтр – это обыкновенный делитель напряжения с нелинейной АЧХ и его можно представить в виде двух сопротивлений:
С помощью делителя напряжения мы можем понизить входное напряжения до необходимого нам уровня.
Формулы для расчета параметров делителя напряжения:
Uвх=Uвых*(R1+R2)/R2
Uвых=Uвх*R2/(R1+R2)
Rобщ=R1+R2
R1=Uвх*R2/Uвых – R2
R2=Uвых*Rобщ/Uвх
Rобщ=10 кОм, Uвх=10 В, на выходе делителя надо получить Uвых=7 В
Порядок расчета:
1. Определяем R2= 7*10000/10= 7000= 7 кОм
2. Определяем R1= 10*7000/7-7000= 3000= 3 кОм, или R1=Rобщ-R2=10-7= 3 кОм
3. Проверяем Uвых=10*7000/(3000+7000)= 7 В
Что нам и требовалось.
Знание этих формул необходимо не только для построения делителя напряжения с нужным выходным напряжением, но и для расчета фильтров нижних и верхних частот, в чем вы убедитесь ниже.
Так как сопротивление нагрузки, подключаемой к выходу делителя, влияет на выходное напряжение, то значение R2 должно быть в 100 раз меньше входного сопротивления нагрузки. Если не нужна высокая точность, то это значение можно снизить до 10 раз.
Это правило также справедливо и при расчетах фильтров.
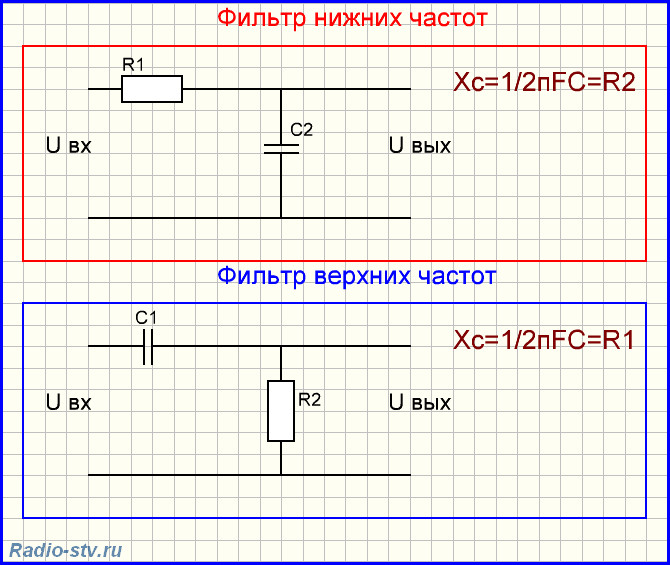
Чтобы из делителя напряжения на двух резисторах получить фильтр применяют конденсатор.
Как вы уже знаете, конденсатор обладает реактивным сопротивлением. При этом его реактивное сопротивление на высоких частотах минимально, а на низких частотах – максимально.
А при замене конденсатором сопротивления R2 (при этом, обладая малым реактивным сопротивлением на высоких частотах, конденсатор шунтирует токи высокой частоты на землю, а на низких частотах его сопротивление велико и ток через него не проходит)- фильтр нижних частот.
Как я уже сказал, уважаемые радиолюбители, мы не будем глубоко нырять в дебри электротехники, иначе мы заблудимся и забудем о чем шла речь. Поэтому сейчас мы абстрагируемся от сложных взаимосвязей мира электротехники и будем рассматривать эту тему как частный случай, не привязанный ни к чему.
Но продолжим. Не так все плохо. Знание хотя бы элементарных вещей очень большое подспорье в радиолюбительской практике. Ну не рассчитаем мы точно фильтр, а рассчитаем с ошибкой. Ну и ничего страшного, в ходе настройки прибора мы подберем и уточним нужные номиналы радиодеталей.
Порядок расчета Г-образного фильтра верхней частоты
В приведенных примерах расчет параметров фильтра начинается с того, что нам известно общее сопротивление делителя напряжения, но наверное правильнее, при практическом расчете фильтров, определять сначала сопротивление резистора R2 делителя, значение которого должно быть в 100 раз меньше сопротивления нагрузки к которой фильтр будет подключен. А также следует не забывать что делитель напряжения тоже потребляет ток, так-что в конце, необходимо будет определить и рассеиваемую мощность на резисторах для их правильного выбора.
Пример: Нам надо рассчитать Г-образный фильтр верхней частоты с частотой среза 2 кГц.
Входное напряжение принимаем за 1, а выходное за 0,7 (можно взять конкретные напряжения, но в нашем случае это никакой роли не играет).
Проводим расчет:
1. Так как мы подключили конденсатор вместо резистор R1, то реактивное сопротивление конденсатора Хс = R1.
2. Определяем по формуле делителя напряжения сопротивление R2:
R2=Uвых*Rобщ/Uвх =0,7*5000/1 = 3500= 3,5 кОм.
3. Определяем сопротивление резистора R1:
R1=Rобщ-R2= 5 – 3,5= 1,5 кОм.
4. Проверяем значение выходного напряжения на выходе фильтра при рассчитанных сопротивлениях:
Uвых=Uвх*R2/(R1+R2) =1*3500/(1500+3500) = 0,7.
5. Определяем емкость конденсатора, которую выводим из формулы: Xc=1/2пFC=R1 —> C=1/2пFR1:
C=1/2пFR1 = 1/2*3,14*2000*1500 =5,3*10-8 =0,053 мкФ.
Емкость конденсатора также можно определить по формуле: C=1,16/R2пF.
6. Проверяем частоту среза Fср по формуле, которую также выводим из выше приведенной:
Fср=1/2пR1C= 1/2*3,14*1500*0,000000053 = 2003 Гц.
Таким образом мы определили, что для построения фильтра высокой частоты с заданными параметрами (Rобщ= 5 кОм, Fср= 2000 Гц) необходимо применить сопротивление R2= 3,5 кОм и конденсатор емкостью С= 0,053 мкФ.
? Для справки:
? 1 мкФ = 10-6 Ф = 0,000 001 Ф
? 0,1 мкФ = 10-7 Ф = 0,000 000 1 Ф
? 0,01 мкФ = 10-8 Ф = 0,000 000 01 Ф
и так далее…
Порядок расчета Г-образного фильтра нижней частоты
Пример: Нам надо рассчитать Г-образный фильтр нижней частоты с частотой среза 2 кГц.
Входное напряжение принимаем за 1, а выходное за 0,7 (как и в предыдущем случае).
Проводим расчет:
1. Так как мы подключили конденсатор вместо резистор R2, то реактивное сопротивление конденсатора Хс = R2.
2. Определяем по формуле делителя напряжения сопротивление R2:
R2=Uвых*Rобщ/Uвх =0,7*5000/1 = 3500= 3,5 кОм.
3. Определяем сопротивление резистора R1:
R1=Rобщ-R2= 5 – 3,5= 1,5 кОм.
4. Проверяем значение выходного напряжения на выходе фильтра при рассчитанных сопротивлениях:
Uвых=Uвх*R2/(R1+R2) =1*3500/(1500+3500) = 0,7.
5. Определяем емкость конденсатора, которую выводим из формулы: Xc=1/2пFC=R2 —> C=1/2пFR2:
C=1/2пFR2 = 1/2*3,14*2000*3500 =2,3*10-8 =0,023 мкФ.
Емкость конденсатора также можно определить по формуле: C=1/4,66*R2пF.
6. Проверяем частоту среза Fср по формуле, которую также выводим из выше приведенной:
Fср=1/2пR2C= 1/2*3,14*3500*0,000000023 = 1978 Гц.
Таким образом мы определили, что для построения фильтра нижней частоты с заданными параметрами (Rобщ= 5 кОм, Fср= 2000 Гц) необходимо применить сопротивление R1= 1,5 кОм и конденсатор емкостью С= 0,023 мкФ.
Т – образный фильтр
Т- образные фильтры высоких и низких частот, это те же Г- образные фильтры, к которым добавляется ещё один элемент. Таким образом, они рассчитываются так же как делитель напряжения, состоящий из двух элементов с нелинейной АЧХ. А после, к расчётному значению суммируется значение реактивного сопротивления третьего элемента. Другой, менее точный способ расчёта Т-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «первого» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента Т-образного фильтра. Если это конденсатор, то значение ёмкости конденсаторов в Т-фильтре увеличивается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек уменьшается в два раза:
П – образный фильтр
П-образные фильтры, это те же Г- образные фильтры, к которым добавляется ещё один элемент впереди фильтра. Всё, что было написано для Т-образных фильтров справедливо для П-образных.
Как и в случае с Т-образными фильтрами, для расчёта П-образных используют формулы делителя напряжения, с добавлением дополнительного шунтирующего сопротивления первого элемента фильтра. Другой, менее точный способ расчёта П-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «последнего» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента П-образного фильтра. В противоположность Т-образному фильтру, если это конденсатор, то значение ёмкости конденсаторов в П-фильтре уменьшается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек увеличивается в два раза.
Как правило, одноэлементные фильтры применяют в акустических системах. Фильтры верхних частот обычно делают Т-образными, а фильтры нижних частот П-образными. Фильтры средних частот, как правило, делают Г-образными, их двух конденсаторов.
Для написания статьи, кроме всего прочего использовались материалы с сайта www.meanders.ru, автором и владельцем которого является Александр Мельник, за что ему большое и бесконечное (меандровское) спасибо.



Вы что,ребят. У меня студенты в технаре таких ошибок не делают. Сдвиг фазы кто учитывать будет? Треугольнички рисовать не учились?
В первом же примере: R1 = Rобщ-R2… да ладно! А √(Rобщ^2 -R1^2) не хотите? И прлучите правильный ответ в 3.57 кОм вместо ошибочных 1.5 кОм. Переделайте, не позорьтесь уж
Здравствуйте! Статья очень понятная большое спасибо автору, но есть некие ошибки и не допания. Во первых ошибка формулы правельней мне кажется эта формула 1/(2*пи*f*R)=C так как на высоких частотах ёмкость должна быть меньше а по вашей получается на оборот если я прав поправте пожалуйста статью а то людей это заводит в заблуждения так же как и меня пока в коментах не увидел формулу. Второй вопрос как быть с R2 если сопротивление нагрузки 4 Ома?
По моему Xc = 1:(2п*f*c)
И
C = 1:(2п*f*x)
Это одно и тоже!
Тоесть обе эти формулы обсалюдно равнозначны.
Здравствуйте подскажите какие параметры конденсатора и резистора необходимо использовать что б сделать г образный фильтр ниских частот под уселитель с выходом 20-20000гц чтобы потключить СПббуфер 40ват.заранее благодарен
Спасибо автору. Очень полезная и нужная статья. Вот бы еще про активные ФВЧ и ФНЧ с применением операционных усилителей.
Можно ли по этой формуле вычислить влияние кабеля на АХЧ, т.е. определить частоту среза по ВЧ и НЧ.
Характеристики кабеля следующие (1 м):
С=55 пФ
R=0,036 Ом
Извините, но мне кажется, что в ваших формулах закралась ошибка:
C=1/2пFR1 => Fср=1/2пR1C
в то время как правильно:
C=1/2пFR1 => Fср=2С/пR1
По какой формуле находится частота среза для RL фильтра нижних частот?
——-
схема: _https://pp.vk.me/c619328/v619328220/404a/28sBu41d1C8.jpg
Заранее благодарен
Доброго дня Alex!
К сожалению, в комментариях я не смогу прописать формулы, а писать новую статью – нет пока времени. Я могу Вам посоветовать посетить вот эту страничку:
_http://www.meanders.ru/filters.shtml
С уважением, Admin.
Здраствуйте!
По всей видимости в этой формуле ошибка, нужно подставлять не R2 а R1
Цитата: – “Емкость конденсатора также можно определить по формуле: C=1/4,66*R2пF”
Объясните пожалуйста, пробовал аналогичные расчёты провести программой “RadioAmCalc 1.20 Free”, результат для Г-образный ФВЧ не совпадает, где ошибка?
Спасибо.
Доброго дня Serwik!
В формуле ошибок нет (я так думаю;).
А чтобы найти истину, давайте вместе посчитаем по Вашим данным.
С уважением, Admin.
У меня не RC, а LC ФНЧ и LC ФВЧ
Для LC ФНЧ узнать частоту среза, данные L=0,09мкГн C=48пф
F=1/2*п*√LC результат умножаем 1000000000 получаем результат в Мгц = 76.6
Для LC ФВЧ узнать частоту среза, данные L=0,06мкГн C=43пф, формула та-же,
результат = 99,1Мгц
Правильно?
Доброго дня Serwik!
Формула, по которой Вы считаете, предназначена для определения частоты резонанса КОЛЕБАТЕЛЬНОГО LC контура. Частота среза LC фильтров определяется не так, более сложновато (одной формулой не отделаться).
С уважением, Admin.
Здраствуйте Админ!
Где прочитать о правильном расчёте, с более менее понятным изложением материала?
Доброго дня Serwik!
По имеющейся емкости и индуктивности определить частоту среза фильтра можно по аналогии фильтра на резисторе и конденсаторе, как в статье, только формулы немного другие.
Конкретно по Г-образному фильтру на конденсаторе и емкости Вы можете прочесть по ссылке:
_http://www.meanders.ru/filters.shtml
С уважением, Admin.
Подскажите, пожалуйста! Как мне определить R_общ?.. А то я совсем тупой овощ.. мне непонятно.
[известна мощность 15W и сопротивление динамика 4Ом]
Здравствуйте Александр!
Извините, но не понятен вопрос.
Что конкретно Вам нужно определить?
С уважением, Admin.
В-общем.. у вас в расчётах написано “Дано: общее сопротивление делителя напряжения 5kOm”, например. Как его определить? Где что замерять, разъясните пожалуйста..
Здравствуйте Александр!
“В приведенных примерах расчет параметров фильтра начинается с того, что нам известно общее сопротивление делителя напряжения, но наверное правильнее, при практическом расчете фильтров, определять сначала сопротивление резистора R2 делителя, значение которого должно быть в 100 раз меньше сопротивления нагрузки к которой фильтр будет подключен”
“Сопротивление нагрузки” – это, к примеру, входное сопротивление усилителя (в промышленных устройствах обычно пишут входное сопротивление).
“100 раз” – лучший вариант, но можно и меньше, но тогда АЧХ фильтра будет хуже.
С уважением, Admin.
А Вы не могли бы привести пример расчета Т – образного фильтра, не могу врубиться как его посчитать, что к чему плюсовать “А после, к расчётному значению суммируется значение реактивного сопротивления третьего элемента”- это как подскажите пожалуйста
1. На практике при разработке фильтра ФНЧ или ФВЧ в схеме уже имеется некое входное сопротивление. Именно сопротивление резистора, а никакое не общее сопротивление делителя. Поэтому перед разработчиком стоит задача добиться ослабления или прохождения сигнала на частоте большей частоты среза, расчитав необходимую емкость.
2. Реактивное сопротивление Xc стало фигурировать в статье только после моих замечаний. До этого насколько я помню было обозначение R2. Подобное обозначение было некорректно.
3. Символический метод расчета цепей переменного тока, как видно из названия, применяется для расчета цепей переменного тока. Очевидно, что в данном случае ток постоянный. Поэтому ФНЧ и ФВЧ вы этим методом не расчитаете. При переменных значениях тока проявляется фазовый сдвиг между значениями напряжения и тока из-за наличия реактивных элементов. Импеданс в этом случае будет описываться комплексным числом, в котором реактивное сопротивление конденсатора будет мнимой частью. При сложении/вычитании комплексных чисел пользуются алгебраической формой записи, а при умножении/делении удобно пользоваться показательной формой (для перевода в нее используют формулу Эйлера).
4. Для Г-образного ФВЧ и ФНЧ результаты будут абсолютно одинаковы. Меняются местами лишь резистор и конденсатор. Соберите схему и убедитесь в этом сами. В одном случае при частоте, большей частоты среза, будет наблюдаться ослабление сигнала. В другом – прохождение сигнала.
Доброго дня wayne coyne!
Ну что, продолжим спор.
1. Имеется не сопротивление резистора, а входное сопротивление устройства на вход которого подключается фильтр. Поэтому в статье указано, что правильнее сначала определить сопротивление резистора R2 делителя напряжения (например, фильтр подключается к входу какого-то усилителя НЧ с входным сопротивлением 100 кОм, тогда сопротивление резистора R2 надо брать номиналом в 1 кОм (в сто раз меньше, но неменее чем в 10 раз (но с худшими результатами)), а потом, зная входное и выходное напряжения, по формулам делителя напряжения определять номинал резистора R1.
2. В статье изменений не было, это Ваша, извините, невнимательность.
3. Если Вас не затруднит, напишите пожалуйста для сайта статью по расчету ФНЧ и ФВЧ символическим методом. Я думаю это будет полезно знать всем радиолюбителям. К тому-же статьи оплачиваются (см. раздел “От читателей”).
4. Не согласен (категорически).
С уважением, Admin.
1. В расчетах ФНЧ и ФВЧ некорректно поставлена задача. В исходных данных фигурирует некое “общее сопротивление делителя напряжения”. Величина, которая не представляет абсолютно никакого интереса для разработчика фильтра. Целью расчета подобных фильтров, как правило, является нахождение емкости конденсатора при заданных частоте среза и сопротивлении резистора. Емкость расчитывается по формуле 1/(2*pi*f*R). Весь расчет умещается в одну формулу. Зачем вам понадобилось его загромождать?
2. В расчетах ФВЧ и ФНЧ ошибочно ставится знак равенства между реактивным сопротивлением конденсатора и активным сопротивлением резистора. В результате вы запутались в своих вычислениях и при расчете ФВЧ в 5-м пункте вместо сопротивления 3,5 кОм использовали сопротивление 1,5 кОм. Реактивное сопротивление конденсатора обозначается как Xc и вместе с сопротивлением резистора эти две величины составляют импеданс. Нельзя путать эти понятия! Кроме того, вас даже не насторожило, что для одинаковых исходных данных для ФНЧ и ФВЧ были получены разные результаты!
3. Что касается символического метода расчета цепей переменного тока, то в интернете приведено достаточно информации по этому поводу. Например, здесь _http://electricalschool.info/spravochnik/electroteh/965-simvolicheskijj-metod-rascheta-cepejj.html
Доброго дня уважаемый wayne coyne! Давайте разбираться.
1. “Целью расчета подобных фильтров, как правило, является нахождение емкости конденсатора при заданных частоте среза и сопротивлении резистора”
Сразу вопрос: “заданная частота среза” – это понятно, сами определяем, а “заданное сопротивление резистора” – не понятно. Какого резистора? Кто задал? Резистора, который включен совместно с конденсатором? Скорее всего Вы этот резистор и подразумеваете. Но в формуле 1/(2*pi*f*R) – R=Хс – реактивному сопротивлению конденсатора, а не сопротивлению резистора, включенного совместно с конденсатором. Отсюда и Ваши слова: “В результате вы запутались в своих вычислениях и при расчете ФВЧ в 5-м пункте вместо сопротивления 3,5 кОм использовали сопротивление 1,5 кОм”
2. “В расчетах ФВЧ и ФНЧ ошибочно ставится знак равенства между реактивным сопротивлением конденсатора и активным сопротивлением резистора”, и еще – “В расчетах ФНЧ и ФВЧ некорректно поставлена задача. В исходных данных фигурирует некое “общее сопротивление делителя напряжения”. Величина, которая не представляет абсолютно никакого интереса для разработчика фильтра”
Прочтите пожалуйста статью повнимательней.
Делитель напряжения – основа расчета фильтра. Задача фильтра – понизить (или повысить) входное (выходное) переменное напряжение до 0,7 на определенной частоте. И только рассчитав сопротивления R1 и R2 делителя напряжения, учитывая, что реактивное сопротивление конденсатора должно быть равно R1 (для ФВЧ) или R2 (для ФНЧ) мы сможем определить номинал конденсатора для заданной нами частоты, и никак иначе. Поэтому-то и принимается значение реактивного сопротивления конденсатора равное сопротивлению резистора R1 или R2.
3. “Что касается символического метода расчета цепей переменного тока, то в интернете приведено достаточно информации по этому поводу. Например, здесь _http://electricalschool.info/spravochnik/electroteh/965-simvolicheskijj-metod-rascheta-cepejj.html”
Честно говоря, я так и не понял, как-же рассчитать ФНЧ или ФВЧ этим методом.
4. “Кроме того, вас даже не насторожило, что для одинаковых исходных данных для ФНЧ и ФВЧ были получены разные результаты!”
Но это и естественно, они не могут быть одинаковые!
Задача ФНЧ – снизить входное напряжение до 0,7 на определенной частоте, а задача ФВЧ – поднять выходное напряжение до 0,7 от входного.
Спасибо большое! Очень полезно!
Все просто и понятно, без мути)